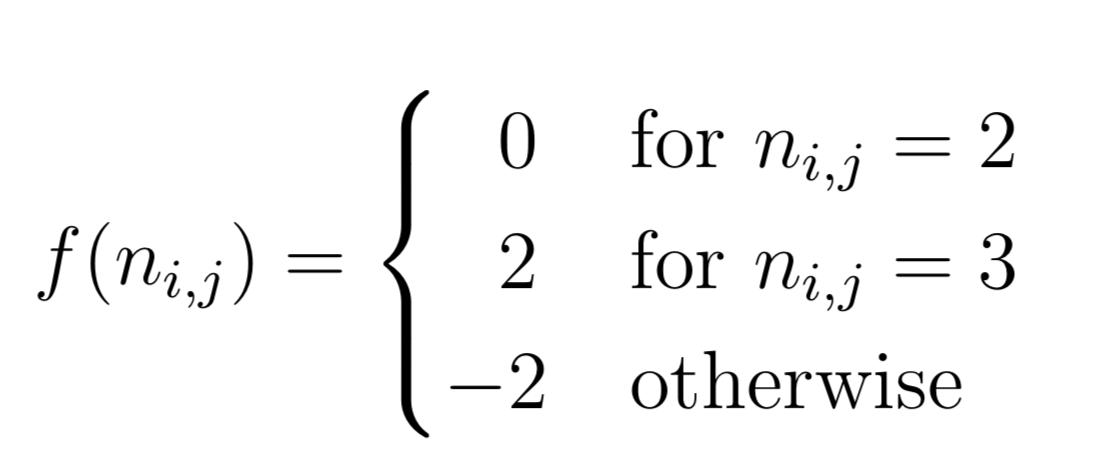This blog post is based on a university project, which I did jointly with my class mate Kathrin Witzlsperger for the course Data Science and Ethics. It is basically an excerpt of our report. The more detailed pdf version can be found here: Report.
1. Introduction
At least since the introduction of the General Data Protection Regulation (GDPR) in the European Union on May 25th 2018, data protection and data privacy are ubiquitous and frequently discussed topics. This shows how important the security of private or confidential data is to both individuals and corporates. Furthermore, globally reported data breaches such as the Facebook - Cambridge Analytica data scandal created an additional consumer sensitivity about where their data is processed and how well it is protected. As today data and lots of computationally expensive operations are processed on remote servers on a daily basis, the need for secure and privacy-maintaining encryption schemes is getting more and more important in order to satisfy not only imposed laws such as the GDPR but also the individual’s need for privacy and anonymity.
One approach to tackle this need is homomorphic encryption that entails the big advantage that computations can be directly performed on encrypted data. This means that, while making use of the computational power of remote servers in the cloud, the data is still encrypted and protected. Hence, privacy and confidentiality can be ensured while interacting with possibly untrusted environments. However, one major drawback is that running these encrypted operations is very time-consuming and memory-intense. That’s why improving the performance of homomorphic encryption and developing new fully homomorphic encryption schemes, that allow an arbitrarily ordered and unlimited number of operations, is a very active research area with huge interest due to numerous potential real world applications.
Within an university project, we explored homomorphic encryption and implemented this methodology for the simple and artificial use case of Conway's Game of Life. The goal was to implement the game using homomorphic encryption for any operation using the Simple Encrypted Arithmetic Library (SEAL) that is maintained by the Cryptography Research Group at Microsoft Research and implements a fully homomorphic encryption scheme in C++.
2. Some Background
Game of Life
Conway’s Game of Life is a cellular automaton developed by the British mathematician John Horton Conway in 1970. It is a zero-player game where based on an initial configuration of a rectangular two-dimensional grid, the board evolves based on predefined rules [5]. In this potentially infinite, orthogonal grid of squares each cell can have one of two possible states: dead or alive. Every cell has eight neighbor cells that are horizontally, vertically or diagonally adjacent to it. There are four rules that determine the state of a cell in the next step (the next generation) based on its own state and the states of its neighbors:
Source: Wikipedia
- Underpopulation: Any live cell with fewer than two live neighbors dies.
- Next Generation: Any live cell with two or three live neighbors lives on to the next generation.
- Overpopulation: Any live cell with more than three live neighbors dies.
- Reproduction: Any dead cell with exactly three live neighbors becomes a live cell.
The first generation is created by simultaneously applying all of these rules to each cell of the initial grid state, which means that deaths and births occur simultaneously in a discrete moment. To generate further generations, one applies the rules repeatedly to the latest grid states. Hence, in the life cycle of the Game of Life each generation depends on the previous one [6].
Homomorphic Encryption
Homomorphic encryption refers to a special type of encryption technique that allows specific computations to be performed on ciphertexts and generate an encrypted result, which, when decrypted, matches the result of those operations performed on the corresponding plaintexts [7]. I don't want to get too much into the maths in this post, but it draws on the mathematical concept of group homorphism, a structure preserving map between two algebraic groups. But they key takeaway is basically, that homomorphic encryption schemes allows a person, let's say Alice, to send a plaintext, which is e.g. encrypted by a cryptographic key, to another person, let's denote him by Bob, to perform expensive operations. Bob can perform operations on this encrypted message without ever being able to read the plaintext or learning about they key and how the message was encrypted. Traditionally, transmitted data needs to be decrypted in order to be processed. After decrypting the data, this can be a point of vulnerability.
3. Approach
General Architecture
The goal of this work is to use homomorphic encryption on Conway’s Game of Life. Following the idea and big advantage of homomorphic encryption that operations can be performed on a remote location without the need of decrypting the data first, it seems obvious to choose a client-server architecture. While the client is responsible for the encryption and decryption of relevant data that is exchanged with the server as well as the display of the current game state in a graphical user interface (GUI), the server performs the operation of determining the next game state that corresponds to the Game of Life’s main logic. To ensure confidentiality of the data, the idea is to encrypt every generation t homomorphically and hand it over to the server afterwards. The server then performs operations on the encrypted data to determine the following grid state of generation t+1 and hands it back to the client. After receiving the encrypted generation t+1, the client decrypts and displays the new grid state in the GUI.
As the grid state of generation t+1 is dependent on the above mentioned update rules that are usually implemented using simple if-else statements, it was necessary to come up with an intermediate step such that the standard operations (multiplication, addition) implemented in the SEAL library could be used to determine the next generation by only working on the encrypted data. To do so, we added an additional encoding scheme on top of the homomorphic encryption in order to be able to perform the computation of the next grid state by just using the add-operation provided by the SEAL. As the state t+1 of a cell is dependent on both its own state and the number of neighbors, both information need to be encoded and considered in the process. The five following illustrate the idea of the encoding scheme.
3.1 Encryption of current grid generation
The state of the Game of Life grid at generation t can be denoted by the matrix A(t), where the state of cell a_i,j ∈ {0, 1} encodes the cell being dead or alive. This is the first component required for the computation outsourced to the server. The matrix A(t) is encrypted by applying the built-in homomorphic encryption function of the SEAL to every element a_i,j of generation t in order to get the encrypted grid matrix A′(t) that contains the ciphertext objects.
3.2 Computation of neighbor matrix
As the second component to obtain the grid state t+1 is the number of live neighbors for each cell, these information need to be computed. For each cell a_i,j, the number of adjacent live cells are counted, captured and stored in the neighbor matrix N(t). Within the neighbor matrix, n_i,j denotes the number of live neighbors of cell a_i,j. To consider neighboring cells that would be outside of the grid’s range, it is assumed, that the left and right as well as the top and bottom edges of the grid are stitched together, yielding a toroidal array. In this way all cells obtain eight neighbors.
3.3 Encoding and encryption of neighbor matrix
In this step, the neighbor matrix N(t) is encoded in a way such that by pairwise addition with the initial board state A(t) it can be decoded to the game state A(t+1) using some predefined rules. In an encryption context these encoding and decoding rules could be seen as the keys that just the client possesses. The neighbor matrix N(t) is encoded by applying the following encoding function f to each element n_i,j.
This results in the encoded neighbor matrix B(t), where each element b_i,j is computed by f(n_i,j). B(t) is afterwards encrypted homomorphically by applying the element-wise encryption function of the SEAL in the same way as in the first step , which results in the encrypted and encoded neighbor matrix B′(t).
3.4 Server-side homomorphic add-operation
After the encryption process, the matrices A′(t) and B′(t) are transmitted to the server within the message m = {A′(t), B′(t)}. The server then simply performs a matrix addition of the two transmitted matrices using pairwise addition with the built-in function of the SEAL.
C′(t) = A′(t) + B′(t) denotes the result of the matrix addition, where c′_i,j = a′_i,j + b′_i,j is still in an homomorphically encrypted state. After this operation the result matrix C′(t) will be transmitted back to the client.
3.5 Decryption and decoding of server response
Once the client receives the server response C′(t), it uses the SEAL to decrypt the result of the matrix addition. In this way the ciphertexts are converted to numerical values that are stored in the matrix C(t).To finally get the state of the grid of generation t+1, the following decoding function g needs to be applied to each element of C(t):
This results in a matrix A(t+1), where each element is either 0 or 1 representing the state of a cell in generation t+1 in line with the rules of Conway’s Game of Life.
4. Implementation
Due to our limited background in C++ (the language SEAL was initially implemented), we implemented the application in Python using PySEAL (https://github.com/Lab41/PySEAL). PySEAL provides a dockerized Python wrapper implementation of the SEALv2.3 using pybind11 [9]. By building an image from the Dockerfile provided within PySEAL the Python package seal is created. This can then simply be imported and used within the also dockerized client-server model implemented in Python.
The code can be found in the following Github repo:
https://github.com/patricktu2/GameOfLifeMeetsPySEAL
5. Conclusion
This work demonstrates homomorphic encryption using the simple example of Conway’s Game of Life. While for the sake of the demonstration the server was simulated locally on the same machine, the practical use cases and implications still became clear.
In times where data is an important asset that can contain sensitive and confidential information, companies and individuals highly mind where their data is processed. Homomorphic encryption could be a way to make use of remote computing power, while still ensuring the privacy of the data. This could have industry-wide applications and implica-tions, especially for economies or societies that are very sensitive towards data privacy and protection such as Germany. However, the main drawbacks of homomorphic encryption are performance-wise. The computing time for encrypted operations increases significantly with the size of the data. IBM faced the same issue with their first attempts at homomorphic encryption, which ran 100 trillion times slower than the corresponding computations on plaintexts. Hence, outsourcing the computation using homomorphic encryption would just make sense when encrypting inputs and decrypting outputs is faster than performing the computation itself. In a recent release of IBM’s library HElib a significant improvement of performance was reached, but for an enterprise- and industry-wide adoption of this technology further developments regarding efficiency still need to be taken. Besides that, most implementations are just partially homomorphic cryptosystems meaning that not all, arbitrary computations on ciphertexts are supported. Nevertheless, homomorphic encryption is a very promising field. Further developments in fully homomorphic encryption, which is still in research phase, could overcome security concerns of cloud computing and enable secure applications, storage and services to be offered regardless of where the servers reside.